Fragt man danach, ob zwei Bilder gleich sind, dann fragt man nach deren Ähnlichkeit, genauer: nach deren Identität. Zwei Bilder sind genau dann identisch, wenn keine unterscheidenden Eigenschaften festzustellen sind. Identität bezeichnet somit den Extrempunkt einer Ähnlichkeitsrelation zwischen zwei oder mehreren Gegenständen, insofern sich identische Bilder nicht nur hinsichtlich mehrerer Merkmale (Ähnlichkeit), sondern aller Merkmale gleichen (Identität). Beim Vergleich zweier digitaler Bilder besteht in der Frage nach deren Identität die Problematik, dass eine Ähnlichkeitsabweichung hier bereits durch unterschiedliche Bildgröße, Auflösung, Kompression etc. entstehen kann. Wie also lässt sich bestimmen, ob zwei digitale Bilder identisch oder zumindest ähnlich sind?
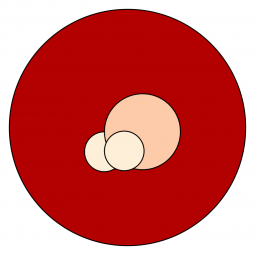
Eine Möglichkeit besteht darin, einen Pixelvergleich vorzunehmen, d.h. Pixel für Pixel zu vergleichen. Hierfür werden die beiden zu vergleichenden Bilder gleichsam übereinandergelegt: Pixel, die denselben Farbwert besitzen, werden schwarz gefärbt, die anderen weiß, so dass die Abweichung, wie das erste Beispiel zeigt, deutlich sichtbar wird. Um dieses Verfahren zu demonstrieren, habe ich ein Bild Piet Mondrians modifiziert, indem ich die gelbe Farbfläche rot eingefärbt habe. Der Pixelvergleich offenbart den Unterschied auf den ersten Blick, zeigt ein weißes Dreieck (= der modifizierte Bereich) auf schwarzem Grund (= der unveränderte Bereich).
Pixelvergleich, Beispiel 1

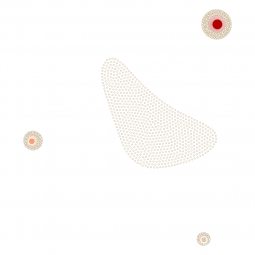
Diese Art des Vergleichs stößt jedoch sehr schnell an seine Grenzen, wie das zweite Beispiel zeigt. Hier habe ich Claude Monets berühmte Seerosen um einen Pixel nach oben verschoben, so dass das gesamte Bild auf der ursprünglichen Bildfläche um einen Pixel nach oben gewandert ist, der obere Bildrand also abgeschnitten wurde und am unteren Bildrand eine ‚leere‘ Pixelzeile entstanden ist. Mit bloßen Auge ist kein Unterschied zwischen den beiden Bildern zu erkennen, doch da aufgrund dieser Verschiebung kein Pixel mehr am selben Platz ist, liefert der Vergleich eine beinahe maximale Differenz, eine weiße Fläche mit wenigen schwarzen Punkten.
Pixelvergleich, Beispiel 2

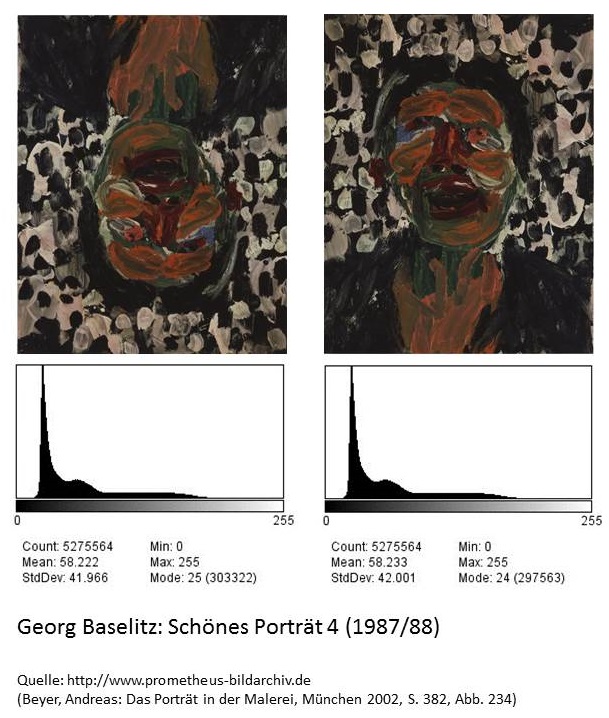
Eine andere Möglichkeit die Ähnlichkeit von Bildern zu bestimmen, besteht darin, deren Histogramme zu vergleichen. Das Histogramm eines Bildes gibt dessen Farbverteilung an, gibt also an, wie oft ein bestimmter Farbwert (RGB) oder Grauwert ((R+G+B)/3) im Bild vorliegt. Diese Verteilung kann als eine Art Fingerabdruck des Bildes betrachtet werden. Da ein Histogramm jedoch lediglich Informationen über die Farbverteilung, jedoch nicht über die Position der Bildpunkte beinhaltet, können verschiedene Bilder dasselbe Histogramm besitzen. Bilder, die gespiegelt oder gedreht wurden, werden aus diesem Grund als gleich erkannt, wie schließlich das dritte Beispiel veranschaulicht.
Histogrammvergleich, Beispiel 3







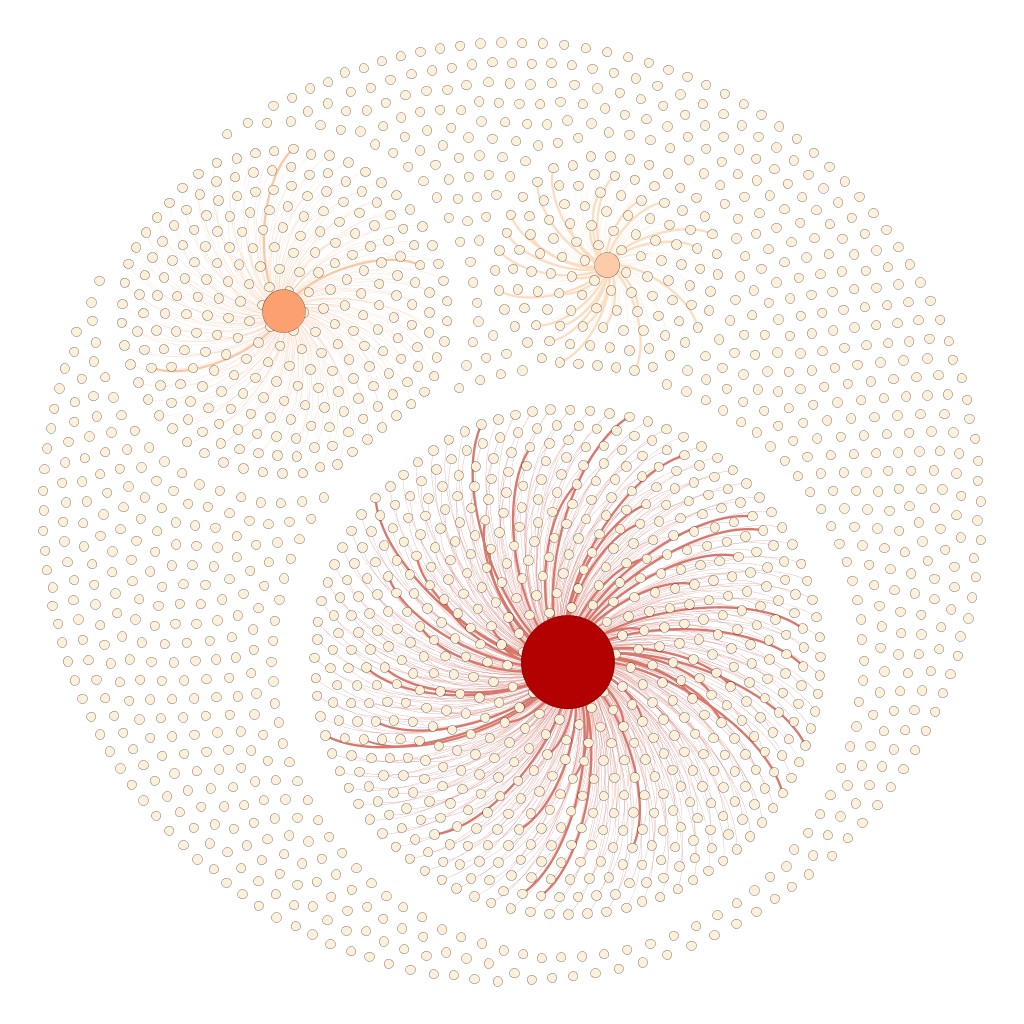
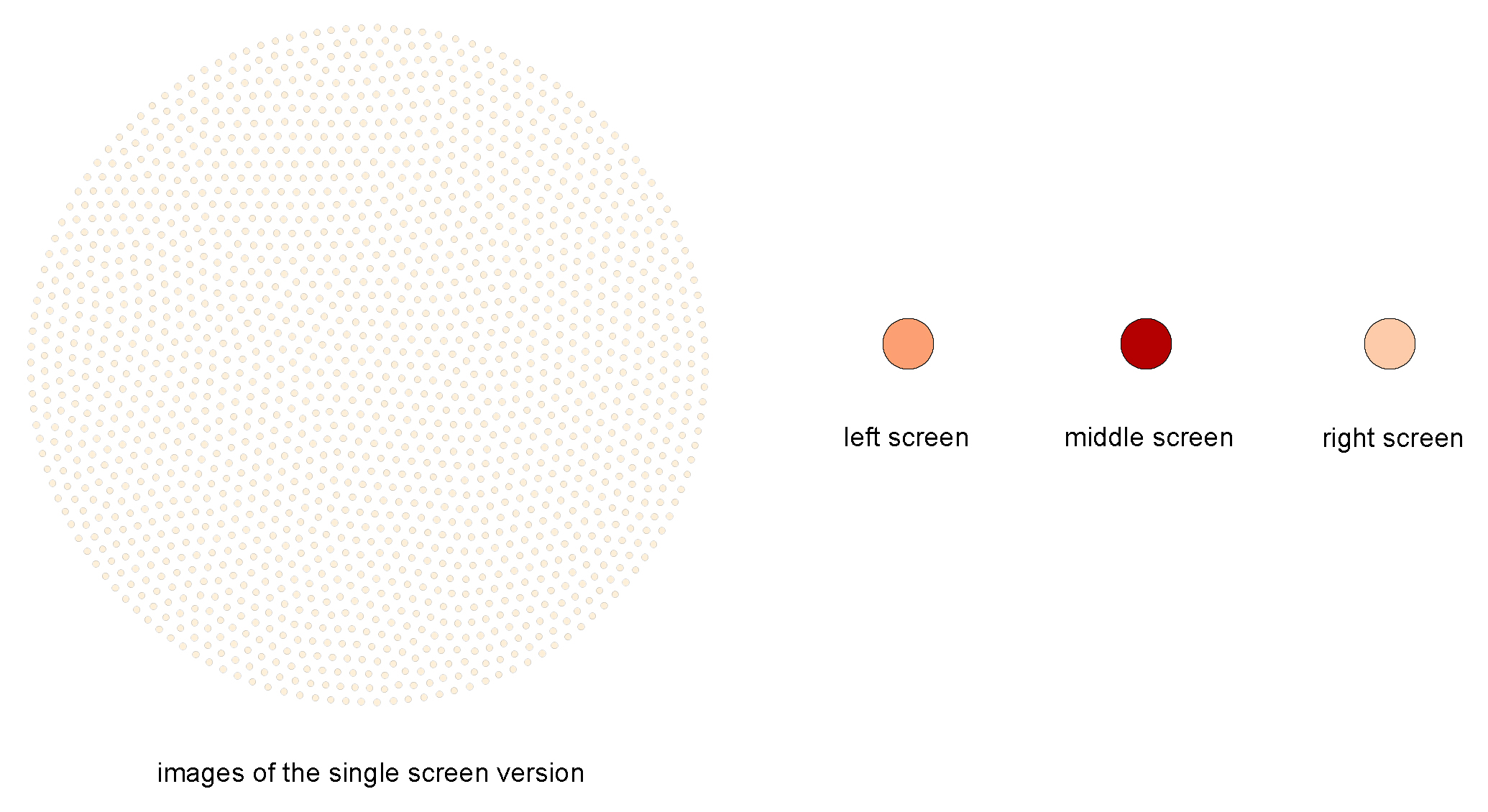
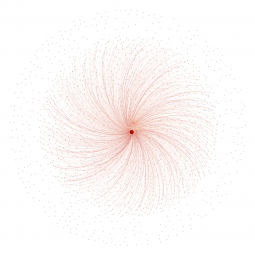
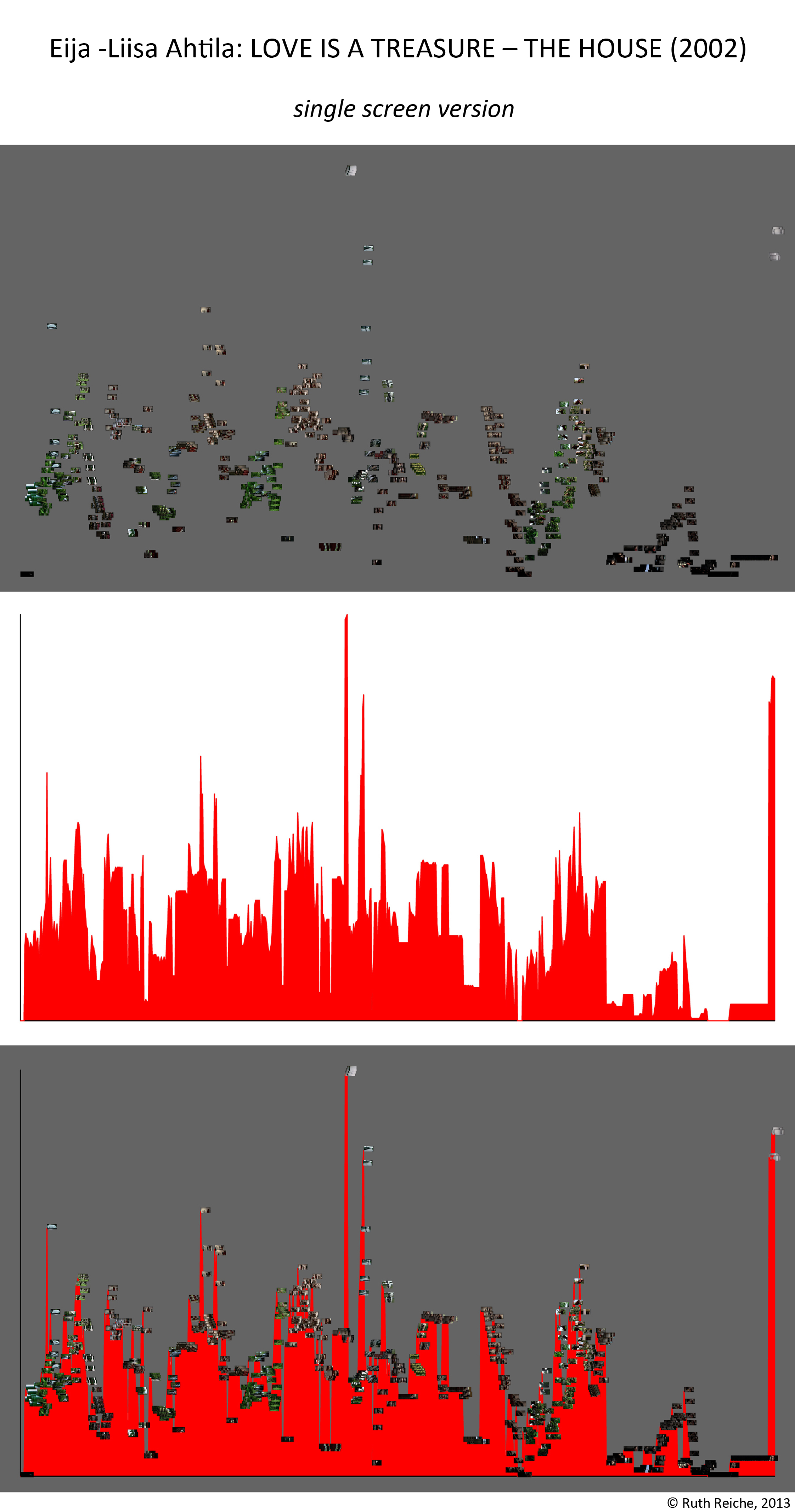
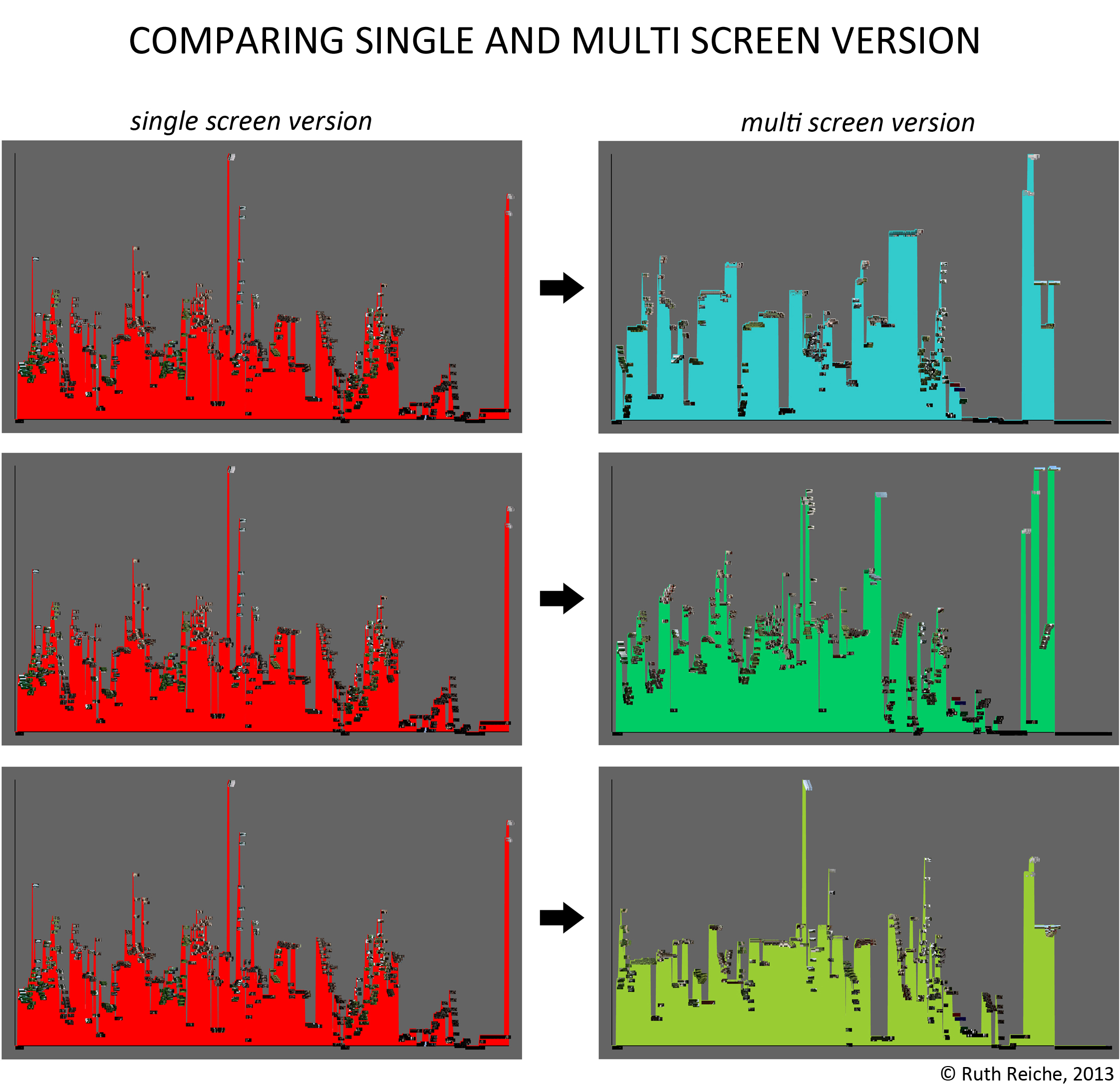
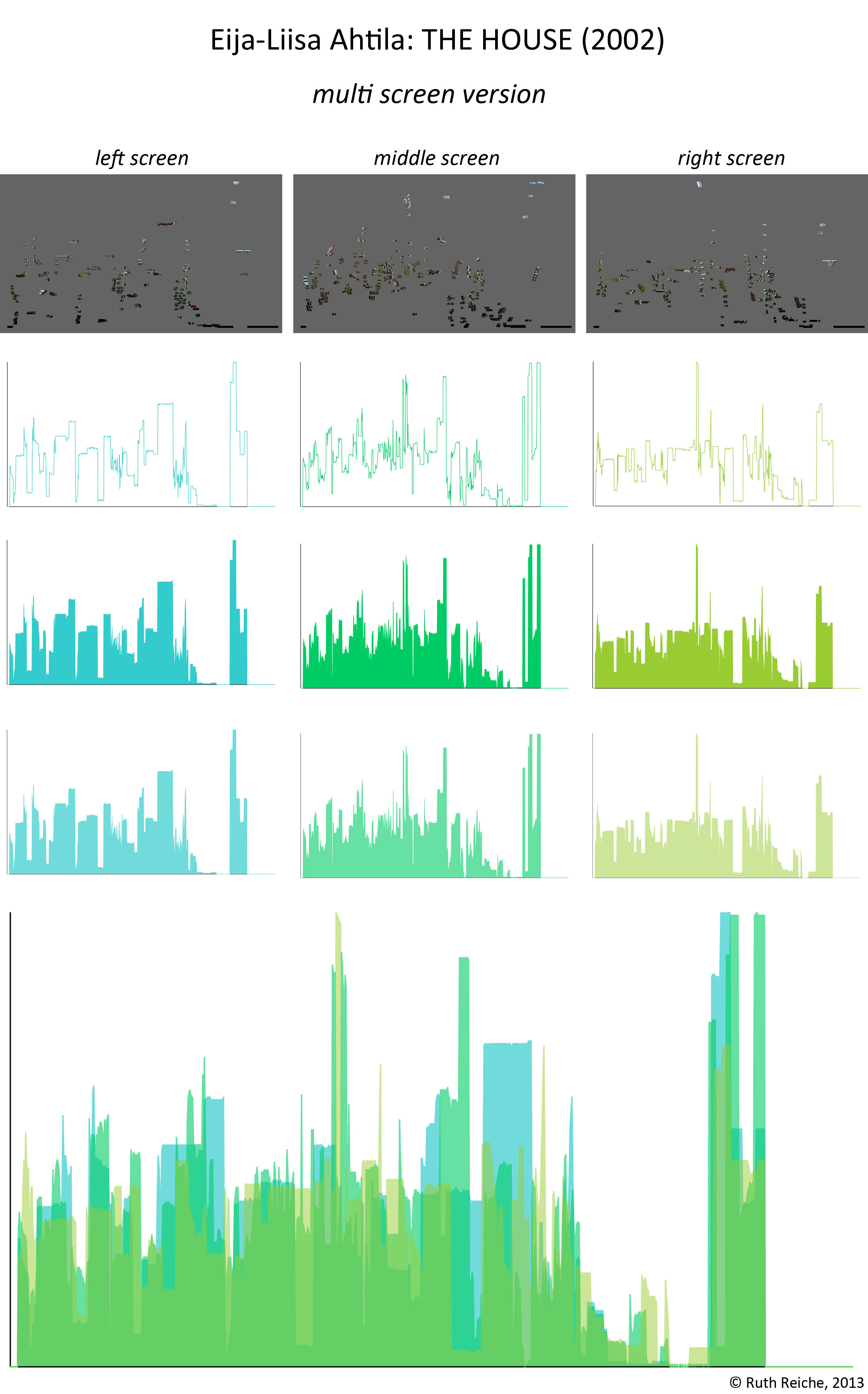
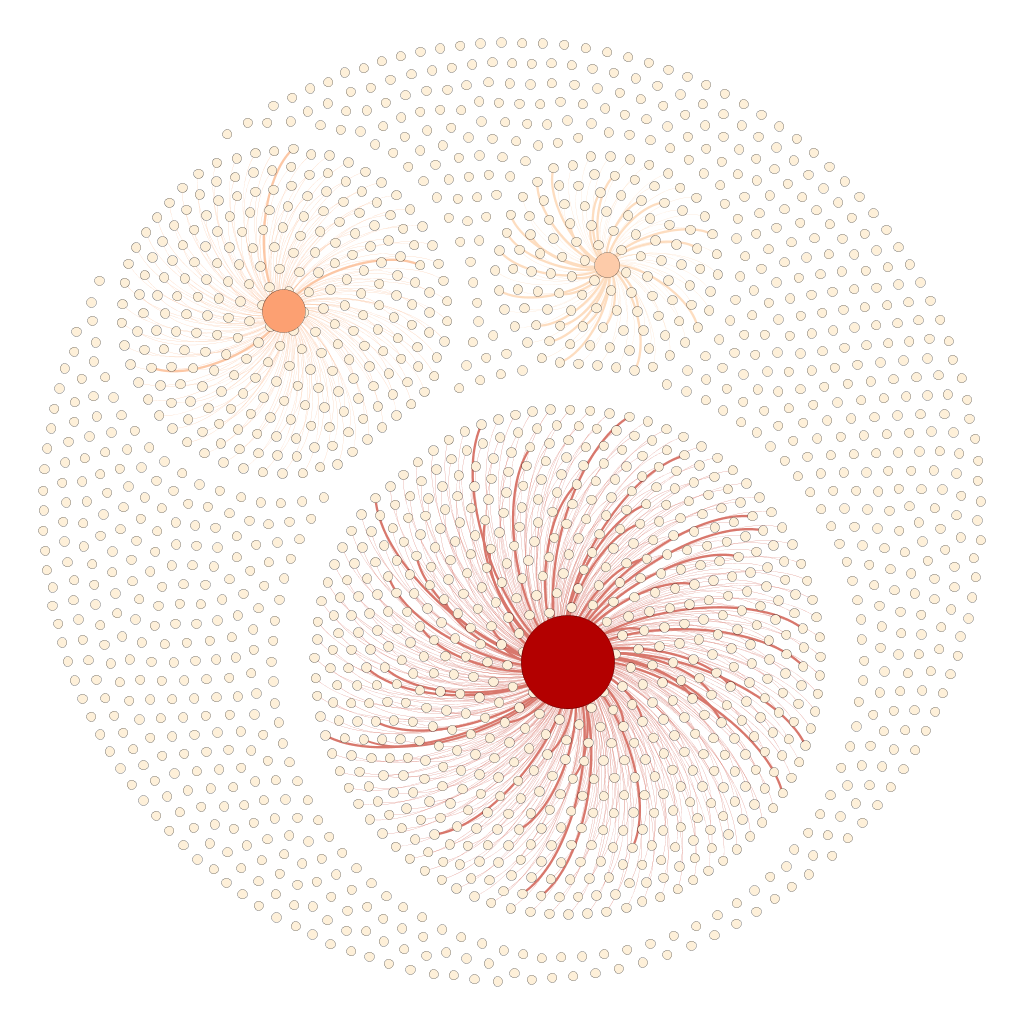 The 1742 images of the single screen version (white dots) are either connected with the left, middle or right screen node (reddish dots) or aren’t connected to anything. Left, middle and right screen node grow with the number of connecting lines. The thickness of those edges again depends on how much the images resemble to each other (that’s because of our image recognition algorithm doesn’t say similiar/not similiar but gives a degree of similiartiy).
The 1742 images of the single screen version (white dots) are either connected with the left, middle or right screen node (reddish dots) or aren’t connected to anything. Left, middle and right screen node grow with the number of connecting lines. The thickness of those edges again depends on how much the images resemble to each other (that’s because of our image recognition algorithm doesn’t say similiar/not similiar but gives a degree of similiartiy).